Dans un premier temps nous verrons ensemble l'énoncé du problème ainsi que le déroulement du programme, nous mettrons ensuite en place ensemble la solution.

Le problème

Objectif

Vous allez rechercher les otages d'un bâtiment donné en sautant de fenêtre en fenêtre à l'aide de votre grappin. Votre but est d'arriver sur la fenêtre de la pièce où les otages se trouvent afin de désamorcer les bombes. Malheureusement vous n'avez qu'un nombre de sauts limités avant que les bombes n'explosent...

Règles

Avant chaque saut, le détecteur vous fournira la direction des bombes par rapport à votre position actuelle :

• U (Up : les bombes sont situées au dessus)

• UR (Up-Right : les bombes sont situées au dessus et à droite)

• R (Right : les bombes sont situées à droite)

• DR (Down-Right : les bombes sont situées en dessous et à droite)

• D (Down : les bombes sont situées en dessous)

• DL (Down-Left : les bombes sont situées en dessous et à gauche)

• L (Left : les bombes sont situées à gauche)

• UL (Up-Left : les bombes sont situées au dessus et à gauche)

Votre mission consiste à programmer le détecteur afin qu'il indique la position de la fenêtre sur laquelle vous devrez vous rendre au saut suivant de sorte que vous atteignez les bombes le plus tôt possible.

Les bâtiments sont représentés par des rectangles de fenêtres, la fenêtre en haut à gauche a pour position (0,0).

Note

Pour certains tests, la position des bombes varie d'une exécution à l'autre. L'objectif est de vous aider à trouver le meilleur algorithme possible.

Les tests fournis et les validateurs utilisés pour le calcul du score sont similaires mais différents.

Déroulement du programme

Entrées du jeu

Le programme doit d'abord lire les données d'initialisation depuis l'entrée standard, puis, dans une boucle infinie, lire depuis l'entrée standard les données relatives à l'état courant et fournir sur la sortie standard les données demandées.

Entrées d'initialisation

Ligne 1 : 2 entiers WH. Le couple (W, H) représente la largeur et la hauteur du bâtiment en nombre de fenêtres.

Ligne 2 : 1 entier N, qui représente le nombre de sauts que vous pouvez faire avant que les bombes n'explosent.

Ligne 3 : 2 entiers X0Y0, qui représentent votre position de départ.

Entrée pour un tour de jeu

La direction vers laquelle se trouve la bombe.

Sortie pour un tour de jeu

Une ligne unique avec 2 entiers XY séparés par un espace. (X, Y) représente la position de la prochaine fenêtre sur laquelle vous devriez sauter. X représente l'index sur l'axe horizontal, Y représente l'index sur l'axe vertical. (0,0) se trouve dans le coin haut gauche du bâtiment.

Contraintes

1 ≤ W ≤ 10000
1 ≤ H ≤ 10000
2 ≤ N ≤ 100
0 ≤ X, X0 < W
0 ≤ Y, Y0 < H
Temps de réponse pour un tour ≤ 150ms
Temps de réponse pour un tour ≤ 150ms

Solution

Analyse du problème

Comme décrit dans l'énoncé, notre algorithme aura pour entrée la direction vers laquelle se trouve la bombe, sous la forme d'une chaîne de caractères. En sortie, on s'attend à recevoir une chaine de caractères qui indique la position du prochain saut sous la forme (x y).

À chaque fois, un retour nous sera fourni nous indiquant la nouvelle direction à suivre, suite à quoi on itérera le déplacement et ainsi de suite jusqu'à ce que Batman arrive sur la bombe.

Le but recherché ici est donc de trouver une valeur x pour laquelle aucune direction 'U' (Up), ou 'D' (Down) ne serait donnée, ce qui signifie qu'elle est égale à la composante x des coordonnées de la bombe.

On peut également appliquer le même raisonnement avec la valeur y que l'on cherche et pour laquelle aucune direction 'L' (Left) ou 'R' (Right) n'est donnée en retour.

Il est possible de visualiser la zone ou le prochain saut peut être effectué en fonction des indications de directions qui nous sont données, comme nous le montre ci-dessous l'image tirée de l'énoncé du problème :

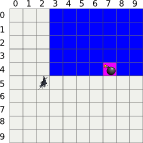
On constate que les valeurs (X, Y) à trouver font partie d'un tableau trié, leurs valeurs allant de 0 à W - 1 pour la composante x et de 0 à Y -1 pour la composante y. La solution que l'on cherche à implémenter correspond bien aux critères nécessaires pour mettre en place une recherche par dichotomie (ou binary search).

La recherche par dichotomie est très intéressante car elle a une complexité de O(log n) contre une complexité de O(n) pour une recherche séquentielle.

Implémentation de l'algorithme

Le but ici est de réduire la zone de sauts possibles en fonction de la direction dans laquelle se trouvent les bombes, jusqu'à arriver sur la bonne case. On sait que si les bombes sont en bas à droite par exemple, rien ne sert de sauter sur la partie en haut et à gauche de la grille. Au lieu de ça, on va sauter au milieu de la zone de sauts possibles afin de voir si l'on a dépassé les bombes ou pas sur chacun des axes.
Le périmètre de la grille de sauts possibles peut se définir par :

$$x_{min} = 0, x_{max}= W -1, y_{min} = 0, y_{max} = H -1$$

On peut ainsi obtenir les nouvelles coordonnées (x, y) à retourner en fonction des coordonnées de la grille de sauts possibles.

$$( x, y ) = \Big( x_{min} + \frac{1}{2}(x_{max} - x_{min}), y_{min} + \frac{1}{2}(y_{max} - y_{min}) \Big)$$

Il ne nous reste plus qu'à écrire le code permettant d'ajuster la taille de la grille de sauts possibles en fonction de la direction communiquée avant de calculer les coordonnées à retourner.

/**
 * Auto-generated code below aims at helping you parse
 * the standard input according to the problem statement.
 **/

var inputs = readline().split(" ");
const W = parseInt(inputs[0]); // width of the building.
const H = parseInt(inputs[1]); // height of the building.
const N = parseInt(readline()); // maximum number of turns before game over.
var inputs = readline().split(" ");
let X0 = parseInt(inputs[0]);  //Initial
let Y0 = parseInt(inputs[1]);

// Setting the coordinates of the possible jumps grid
let minX = 0;
let minY = 0;
let maxX = W - 1;
let maxY = H - 1;

// game loop
while (true) {
  const bombDir = readline(); // the direction of the bombs from batman's current location (U, UR, R, DR, D, DL, L or UL)

  // Adjusting vertical coordinates of possible jumps grid
  if (bombDir.includes("U")) {
    maxY = Y0 - 1;
  } else if (bombDir.includes("D")) {
    minY = Y0 + 1;
  }
  // Adjusting horzontal coordinates of possible jumps grid
  if (bombDir.includes("L")) {
    maxX = X0 - 1;
  } else if (bombDir.includes("R")) {
    minX = X0 + 1;
  }

  // New location to jump  
  X0 = Math.floor(minX + (maxX - minX) / 2);
  Y0 = Math.floor(minY + (maxY - minY) / 2);



  // the location of the next window Batman should jump to.
  console.log(`${X0} ${Y0}`);
}